Failles transformantes et modèle de la tectonique des plaques

Travail réalisé par :
- Nathalie Parquet (Lycée Pablo Picasso - Perpignan)
- Jean Minier (Lycée Pablo Picasso - Perpignan)
- Marc Tartière (Lycée Paul Valéry - Sète)

Niveau : Lycée - Première EDS SVT
Objectif : Proposer un modèle en plaques rigides en utilisant la géométrie des failles transformantes océaniques.

La détermination de l’épicentre d’un séisme (Northern Midle Atlantic Ridge / 06.06.2009 / 20 h 33 28 s /23.87°/-46.11°) enregistré par les stations du réseau "Sismo à l’école" PERF, GABY, QTOE permet de localiser une faille transformante océanique.
L’utilisation d’un modèle analogique simple permet de comprendre que les mouvements des plaques au niveau des dorsales sont des rotations de pièces rigides se déplaçant sur une sphère.

PREMIÈRE ÉTAPE : LOCALISATION DE L’ÉPICENTRE D’UN SÉISME

1° - Détermination de la distance de chaque station à l’épicentre

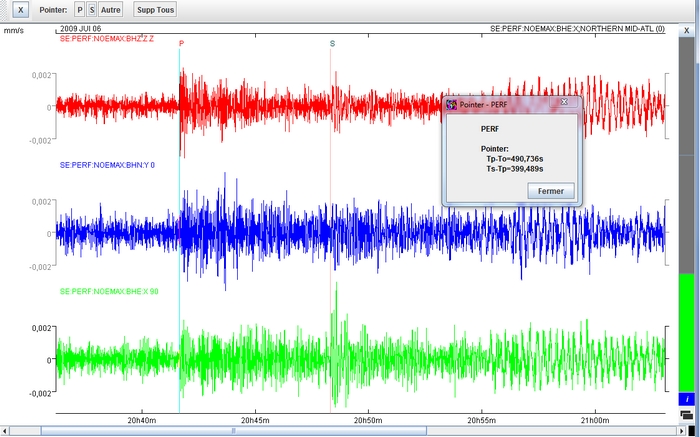
Afficher les ondes (Z, N et E) reçues par la station PERF (Perpignan). Filtrer ente 0,05 et 0,2 Hertz. Pointer les Ondes P et S et déterminer la distance épicentrale. Procéder de la même façon pour GABY (Guadeloupe) et QTOE (Quito).

Tracés pour PERF

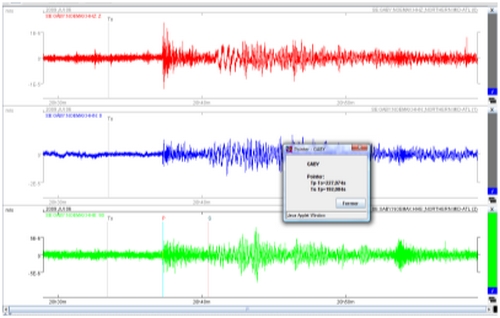
Tracés pour GABY

Tracés pour QTOE

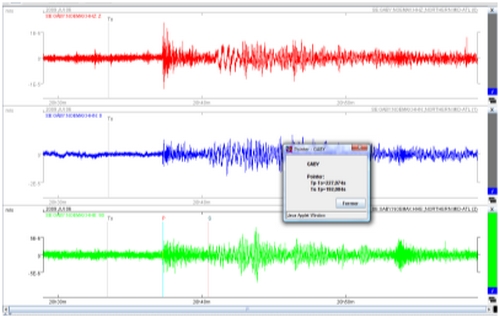
Les résultats obtenus

SeisGram2k permet ensuite de déterminer les distances à l’épicentre en utilisant l’hodochrone.

 
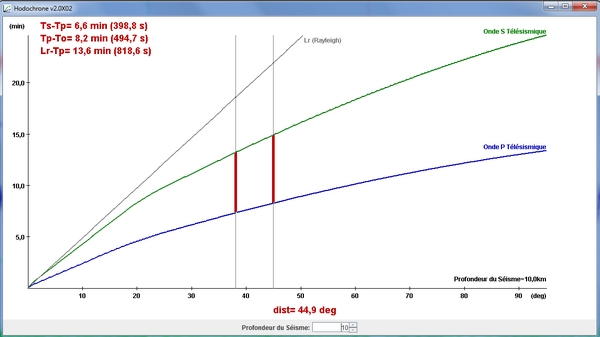
2° - Localisation de l’épicentre par la méthode des cercles.

•     Ouvrir Educarte et afficher les trois stations.
•     Localiser l’épicentre par la méthode des cercles

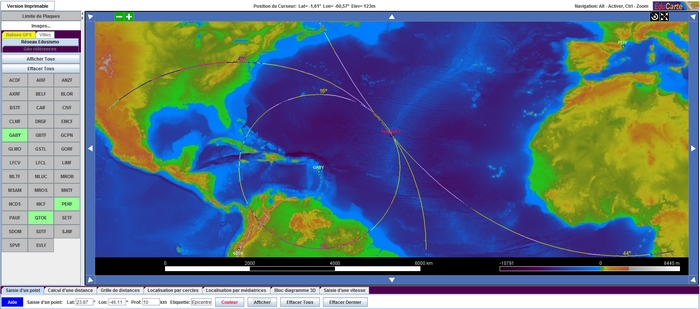
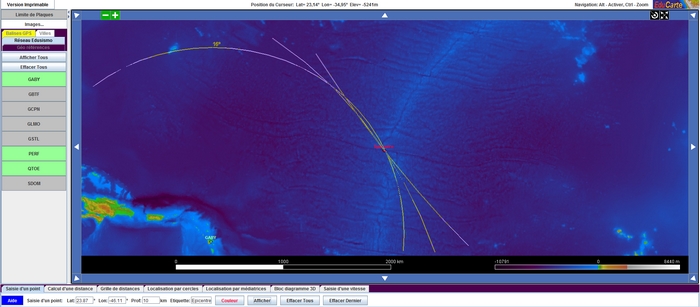
•     Vérifier la précision du travail en saisissant les coordonnées du séisme telles qu’elles ont été déterminées par les sismologues, soit Lat 23.87° et long - 46.11°.
•  Préciser la localisation du séisme sur une faille qui décale l’axe de la dorsale.

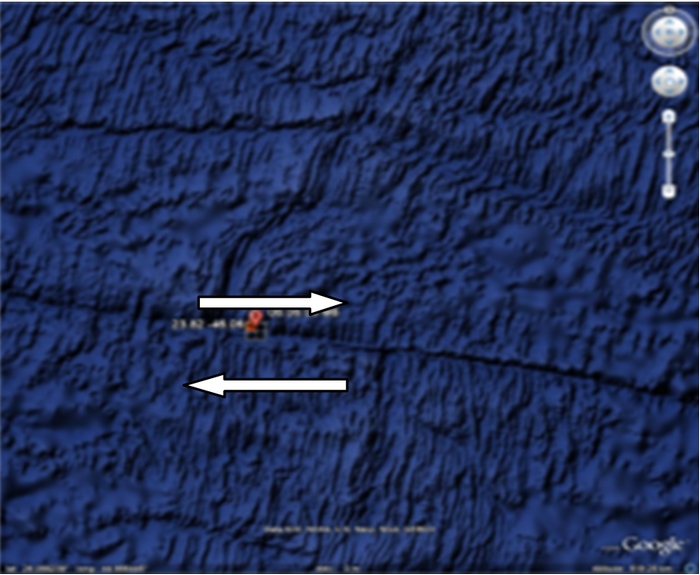
Position de l’épicentre dans Google Earth

Position de l’épicentre dans EduCarte

Variantes possibles pour localiser les failles transformantes à partir des séismes enregistrés :

• Aller sur Google Earth et pointer l’épicentre en utilisant les coordonnées du point.
• Télécharger le fichier KML de sismo à l’école pour ce séisme (l’épicentre est placé).
• Demander à Educarte d’afficher la sismicité > 2. Dézoomer.

Les failles transformantes situées près de l’équateur sont associées à de nombreux séismes entre deux plaques. Ces failles transformantes décalent la dorsale.

DEUXIÈME ÉTAPE : MODÉLISATION DE L’ORIGINE DES FAILLES TRANSFORMANTES

Problèmes :

• Quelle est l’origine de l’activité sismique au niveau de ces failles ?
• Quels sont les apports de la présence de ces failles pour la compréhension de la tectonique des plaques ?

Avec un modèle analogique, les élèves doivent en venir à l’idée que les plaques étant rigides, leur mouvement sur une sphère est donc une rotation dont le centre est le pôle eulérien.

Il est possible de faire un TP « mosaïque » où les élèves travaillent sur des dorsales différentes et mettent ensuite en commun les différents pôles eulériens trouvés.

1° - Détermination du pôle eulérien de la dorsale médio-atlantique sur laquelle se trouve le séisme étudié.

Logiciel utilisé : Educarte

Démarche :
- Choisir deux points de part et d’autres de l’axe de la dorsale sur deux failles transformantes différentes (soit 4 points au total, nommer 1,2,3 et 4). Attention, il faut bien rester sur cette partie de la dorsale car la dorsale nord-atlantique et la dorsale sud-atlantique possèdent un autre pôle eulérien.

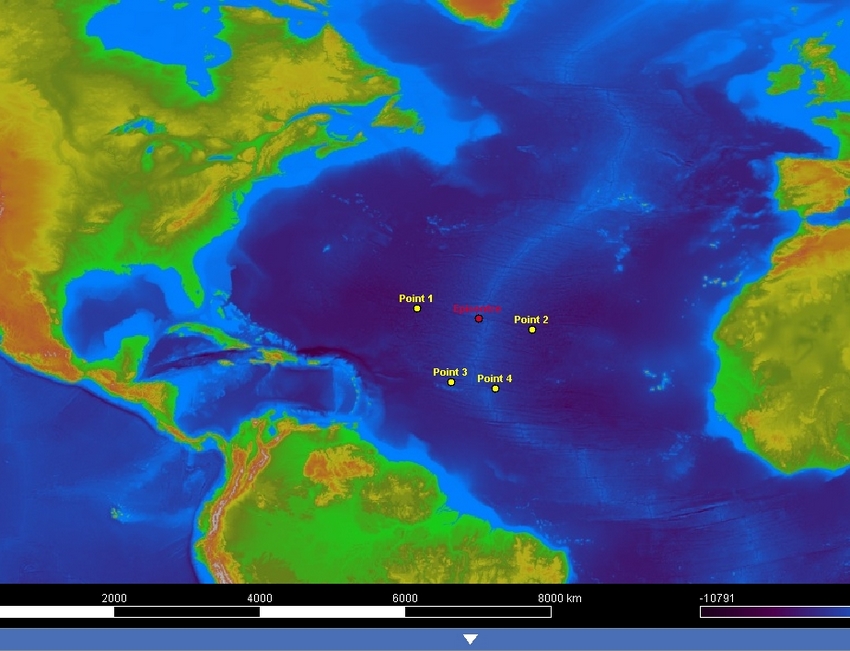
- Tracer la médiatrice entre ces deux points pour chacune des deux failles, soit deux médiatrices au total.

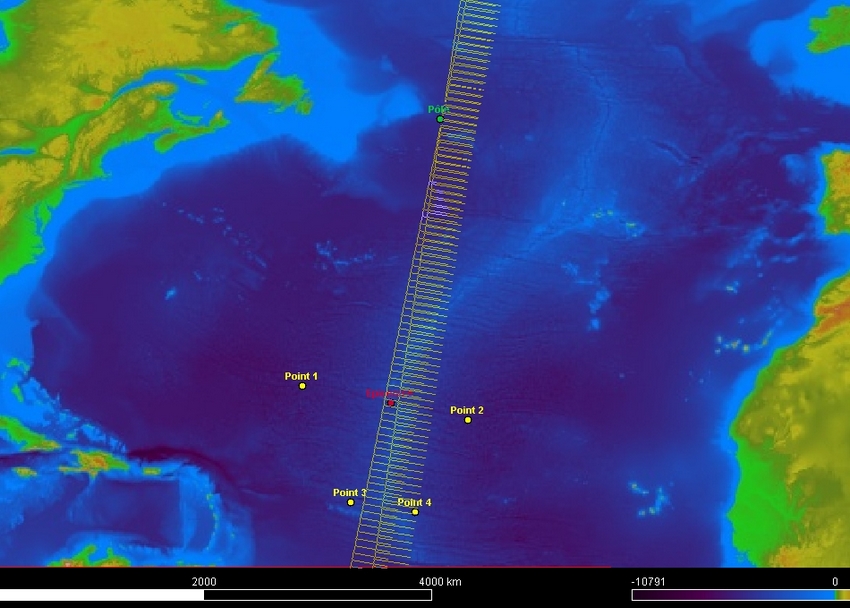
- Positionner le pôle eulérien comme étant le point de rencontre des deux médiatrices (pôle sur l’image écran).
Voici les coordonnées approximatives du pôle : 44.9°en latitude et -40.7° en longitude

2° - Vérification d’un pôle eulérien unique pour toutes les failles transformantes de cette dorsale médio-atlantique.

Pour cela, il suffit de tracer des cercles partant du pôle eulérien et de vérifier que les transformantes sont sur ces cercles.

 
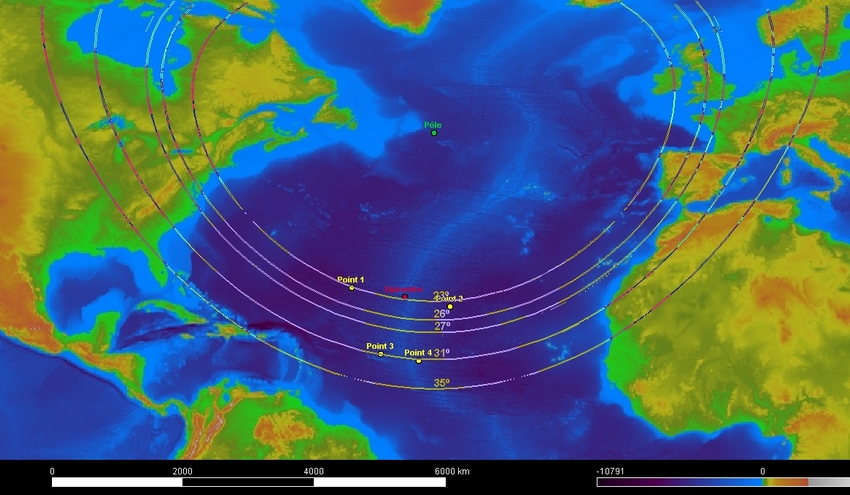
3° - Modélisation du pôle eulérien et l’origine des failles transformantes.

• Matériel nécessaire par modèle :

    ½ globe en polystyrène
    2 Bandes de plâtre médical modélisant deux plaques
    Un système de fixation de ces bandes et une aiguille
    Un emporte-pièce pour faire les trous dans les bandes de plâtre

• Déroulement :

Au début de l’expérience, les deux plaques sont jointives. Tracer un point sur le globe au niveau de chaque trou.

Le modèle simule une dorsale, les deux plaques s’écartent ensuite, l’une de l’autre, avec une vitesse angulaire, ω, qui est la même partout (prendre 3 mesures pour un angle de 10°, 20° puis 30°).
A chaque mesure, il faut tracer un nouveau point sur le globe.

Il est ensuite possible de rejoindre ces points par un tracé au crayon.

•  Interprétation :

Sur le modèle, le pôle eulérien est le point où sont rattachées les deux plaques.
Les déplacements des plaques sur la Terre, qui est une sphère, sont des rotations à partir d’un axe eulérien (et non de simples translations).
L’axe eulérien est l’axe passant par le centre de la Terre autour duquel la plaque tourne. Cet axe virtuel traverse la surface du globe en deux points appelés pôle eulérien de rotation.
En fonction de la distance au pôle eulérien, la vitesse linéaire sera différente pour une même vitesse angulaire selon la relation :
V = R ω
avec V= vitesse linéaire en m/s
R = rayon du cercle = distance à l’axe de rotation
ω = vitesse angulaire en rd/s (π rd = 180 °)

Au niveau du pôle eulérien de rotation, R=0 donc V= 0.
Plus on s’éloigne du pôle, plus R augmente et plus V augmente.

• Conclusion :

- Pour un même système de failles, la vitesse angulaire est la même. En revanche, les vitesses linéaires sont différentes.
- Si les plaques n’étaient pas rigides, elles se déformeraient et il n’y aurait donc aucune rupture.
- Les failles transformantes sont bien la preuve de la rigidité de plaques se déplaçant sur une sphère (dont l’axe est un axe Eulérien).

1 = Point de départ : Les bandes de plâtre modélisent deux plaques rigides.
2 = La dorsale est active : les plaques s’écartent. Pour une même vitesse angulaire, la vitesse linéaire est différente.
3 = La faille transformante, à l’origine d’un séisme, apparaît et décale l’axe de la dorsale.

Ce modèle permet de « retrouver » l’observation de départ au niveau de la dorsale (Ci-dessous, la dorsale au niveau de l’Atlantique central).

Variante possible :

Détermination de la position des pôles eulériens avec le logiciel Tectoglob Exemple : la dorsale Est-indienne

Pour déterminer le pôle eulérien, il faut tracer des tracés d’arc de grand cercle perpendiculaire aux failles transformantes. L’intersection des tracés donne la position (approximative) du pôle eulérien. Pour cet exemple, on trouve les coordonnées suivantes : 14°N et 49° E.

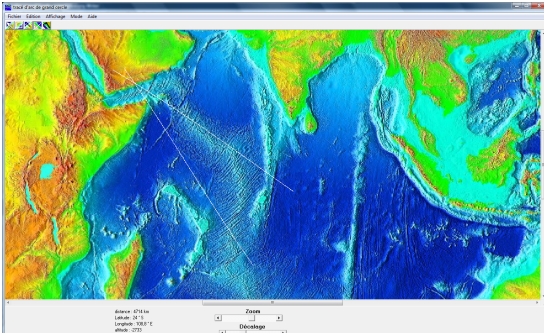
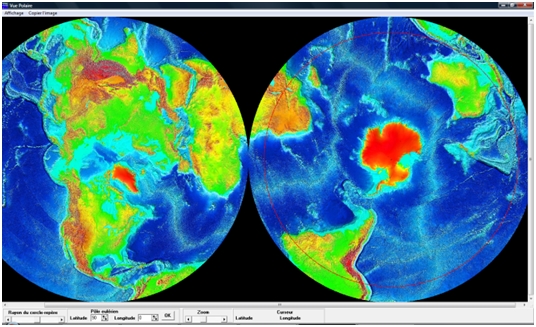
On peut ensuite observer le globe en vue polaire avec le pôle eulérien trouvé. Cette vue permet de vérifier que toutes les failles transformantes de la dorsale se situent sur les cercles formés à partir du pôle eulérien.

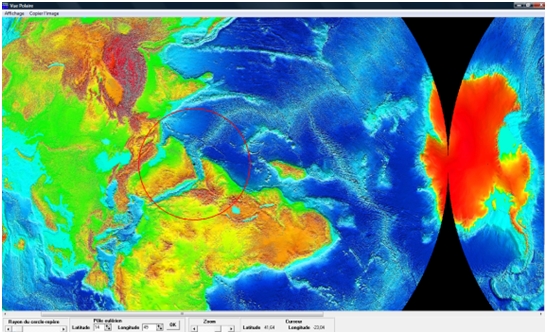
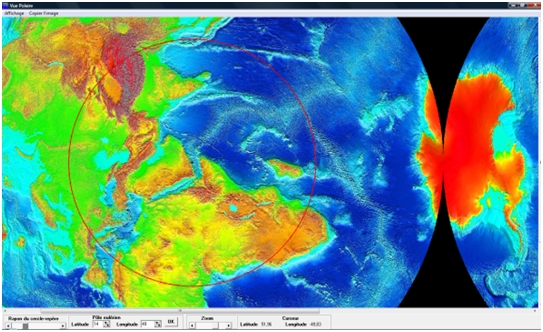
On peut également observer les mêmes failles transformantes en prenant le pôle nord comme pôle eulérien pour la vue polaire. On s’aperçoit que les cercles ne correspondent plus aux failles.