Cours de physique-chimie en vidéos
Cours de physique-chimie en vidéos
M. Gilh Claude enseigne la physique-chimie au lycée Jean Monnet de Montpellier. Afin d’accompagner la continuité pédagogique, il met à disposition ces vidéos de cours.
Elles peuvent être proposées aux élèves afin qu’ils puissent les visionner en autonomie.
1. Lentilles convergentes (4h)
Cours sur les lentilles convergentes. Expériences sur banc optique pour trouver les relations de conjugaison , de grandissement. Théorème de Thalès. Tracé des rayons et principe de formation d’une image. Modèle et principe de mise au point de l’œil et de l’appareil photo.
2. Réfraction : onde et construction Descartes ( 1 heure 14 min)
Expérience de réfraction d’un rayon lumineux. Etablissement des relations de la réfraction de Descartes en considérant la lumière comme une onde dont la vitesse de propagation dépend du milieu. Extension du modèle ondulatoire au modèle géométrique des rayons lumineux en considérant les rayons comme perpendiculaires aux surfaces d’onde. Partie rappel de 2nde et connexion aux notions d’onde de 1ere . Connexion entre deux modèles physique en optique.
3. Interprétation géométrique Descartes (42 min)
Interprétation de la réfraction des rayons par la construction géométrique de Descartes. Étude des quatre situations possibles de la relation des sinus de Descartes par l’analyse des constructions géométriques. Exercice type sur la réfraction. Rappel et développement des notions de 2nde en vue de l’établissement théorique de la relation de conjugaison de la lentille mince dans le 4. afin de retrouver théoriquement les résultats trouvés expérimentalement au 1.
4. Démonstration théorique Descartes (36 min)
Établissement de la relation du dioptre sphérique par la relation de Descartes. Établissement de la relation de conjugaison de la lentille mince en utilisant la relation de conjugaison du dioptre sphérique, et des approximations de Gauss sur les rayons. Description de la vergence de la lentille par l’analyse des rayons de courbures de la lentille. Conclusion et fermeture logiquement cohérente des résultats du 1.
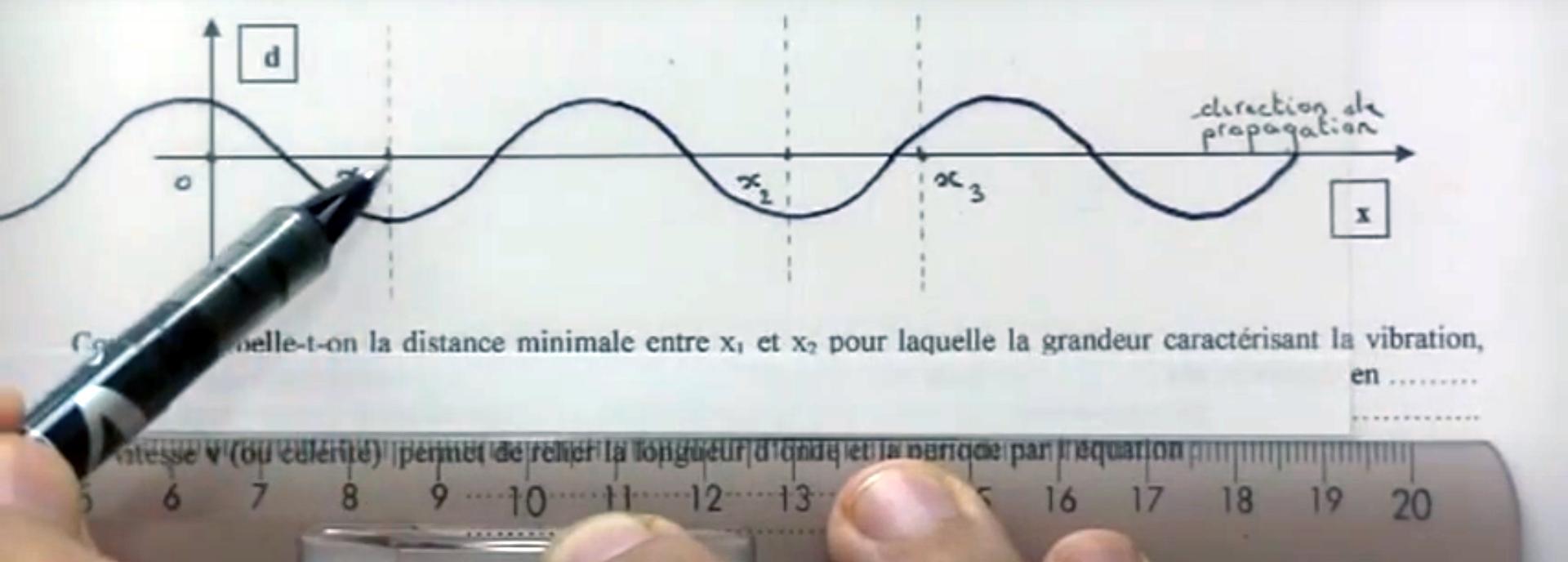
5. Modèle ondulatoire la lumière (40 min)
Établissement d’un modèle simple pour une onde sinusoïdale, définition de la fréquence, de la longueur d’onde, établissement de la relation λ0 . ν = C pour une onde se propageant dans le vide, explication physique de la constance de la fréquence ν au cous d’un changement de milieu, établissement de la relation λ . ν = v pour une onde se propageant dans un milieu homogène. Rappel de la relation n = C / V nécessaire au 6° dispersion lumineuse.
6. Dispersion de la lumière (20 min )
Expérience de dispersion de la lumière blanche par un prisme et interprétation d’une relation de dispersion par l’explication de la dépendance de la vitesse de phase de la lumière dans un milieu dispersif en fonction de la fréquence de l’onde.
7. Interférences lumineuses (1 heure)
Démonstration théorique de l’expression de l’interfrange dans le cas des fentes d’Young. Le modèle de l’onde plane progressive y est développé entièrement de façon à permettre le traitement mathématique des interférences. La grandeur vibratoire est scalaire, on ne s’est pas étendu sur la nature de la grandeur vibratoire …. Explicitation du principe de superposition et explicitation de la différence de marche. Le niveau est accessible à un bon TS.
8. Courants électriques (2 heure 9 minutes )
Introduction à la notion d’intensité et de tension. L’intensité est présentée comme un débit d’électricité au travers d’un conducteur, conducteur caractérisé par une densité de charges libres de ce déplacer sous l’influence d’un champs électrostatique, engendré en tous points du circuit par un générateur. L’accent est mis sur la conservation du débit dans tout le circuit, ce qui permet de monter que la vitesse des porteurs de charge est plus grande dans la résistance, du fait d’une densité de charge libre moindre. On en déduit successivement que dans une résistance les forces de frottements sont plus grandes, de même pour la force électrique et son travail. Enfin les forces étant conservatives, on associera une variation d’énergie potentielle électrique non nulle au bornes de la résistance, alors que cette variation d’énergie sera quasi nulle aux bornes d’un conducteur. La tension peut alors être définie comme une variation d’énergie potentielle électrique par unité de charge.
9. La mole et l’unité de masse atomique.
Élaboration et propriétés des systèmes d’unités en chimie : La mole et l’unité de masse atomique. Comment et pourquoi ces deux systèmes d’unités ont-ils été crée, dans le but de faire des liens entre le monde microscopique des atomes et le monde macroscopique lié à notre échelle.
10. La relativité restreinte ( 2 heures 5 minutes )
Historique de la relativité restreinte et élaboration des relations de transformation de Lorentz. Une étude complète et détaillée qui a amené les scientifiques a concevoir les nouveaux rapports existant entre l’espace et le temps : l’invention d’une « chronogéométrie ».
11. Théorème de Thalès (27 minutes )
Un classique incontournable ! Niveau collège. La démonstration ex nihilo !
12. Consonance et gamme de Pythagore (50minutes)
Étude de la consonance – niveau TS …….. deuxième partie en construction. Une approche théorique de la notion de consonance en lien avec les mathématiques et la physique.
13. La construction de la gamme de Pythagore ( 2 heures 4 minutes )
Construction mathématique de la gamme de Pythagore. Une étude approfondie et détaillé des liens entre la gamme de Pythagore, la physique et les mathématiques.
14 .Transformation et avancement chimique (1 heure 30 min)
Notions de transformations chimiques, réactif en défaut, de tableau d’avancement expliqué de façon très détaillé en vue de l’illustrer sur un exemple concret : le titrage d’une solution de diiode I2 par une solution de thiosulfate de sodium, réalisée et filmée en salle de classe et contenant toutes les consignes expérimentales indispensables pour la réaliser ….. Le niveau est celui d’une 1ère et peut être bénéfique aussi pour une TS.
15. Cours de logique mathématique ( 2h 56 minutes )
Un cours complet sur les différents types de démonstrations utilisés en mathématique. Niveau seconde à terminale. Le contenu de l’exposé montre la construction et la démonstration rigoureuse des différents types de raisonnements mis en œuvre en mathématique.