Newsletter des Laboratoires de Mathématiques #8
Diverses activités proposées à l’ensemble des coordonnateurs des labomaths ont rythmées cette journée.
Après l’annonce du programme de la journée, Mme Dupraz et M. Delwarde, IA-IPR, ont présenté le dispositif « Notre Ecole Faisons la Ensemble ».
https://eduscol.education.fr/3595/notre-ecole-faisons-la-ensemble
Les laboratoires de mathématiques peuvent être un levier pour impulser une réflexion autour de projets prenant place dans ce dispositif.
Les participants ont pu s’exercer à quelques jeux mathématiques, ramenés d’une visite au MMACA (Musée des mathématiques à Cornella del Llobregat), évoqué dans la précédente newsletter. https://mmaca.cat/
Par exemple, un puzzle pouvant être proposé aux élèves de 6e afin d’associer différentes représentations des nombres 0,1 – 0,2 – 0,25 – 0,5 – 0,75 ou encore celui sur les décompositions en produit de facteurs premiers à d’autres niveaux.
Ensuite, monsieur Nicolas Mattiuzzo nous a apporté un regard mathématique différent sur le Rubik’s Cube, à travers des rotations et permutations, théorie des groupes. Un interlude calculatoire nous a permis de travailler des transformations conduisant à quelques représentations. Même si nous n’avons pas réussi à résoudre le Rubik’s Cube, nous avons vraiment tous appréciés cet atelier.
Pour clore la matinée, nous avons proposé la création d’une feuille de route. Les discussions enrichissantes que nous avons eues nous amènent à créer un document de partage sur tribu pour consigner les diverses sorties, lieux d’exposition, …pour les professeurs, comme pour les élèves.
L’après-midi fut consacré à une conférence de M. Ducharme Gilles, professeur émérite, au sujet de la loi de Newcomb-Benford, une Belle au bois dormant mathématique. Après des prolégomènes, et un petit jeu, avec quelques rappels (PSC: Premier chiffre significatif, log10, …) nous avons appris comment S.Newcomb a mis en évidence cette loi à partir des tables de logarithmes, en y associant des probabilités. Les PCS d’une série de nombres choisis au hasard n’apparaissent donc pas de façon uniforme. Cela permettrait de déterminer si les nombres d’une série sont bien des “nombres naturels".
Dans la suite de l’exposé, nous apprenons que c’est F.A.Benford qui met en évidence l’ubiquité de cette loi qui apparaît dans de nombreux phénomènes.
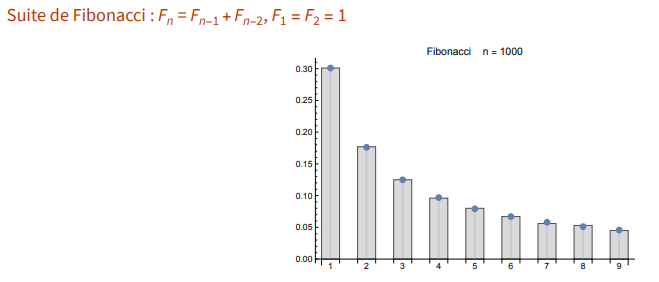
Depuis les années 1990, l’application principale de cette loi intervient dans la détection d’anomalies, de fraudes, plus actuellement à propos des données diverses sur le Covid.
Les documents capturés sont issus du diaporama que nous a communiqué M. Ducharme et que nous avons déposé sur Tribu. Vous pourrez relire les contributions du professeur à ce propos.
Nous remercions l’ensemble des participants dont le dynamisme et l’implication ont fait de cette troisième rencontre un agréable moment !